Introduction

On va parler de suites de Goodstein et d’hydre de Lerne. En particulier on exposera l’intéressant théorème 1 qui contient l’équation [eq-zero]. Mais à dire vrai c’est surtout un prétexte pour donner quelques exemples d’utilisation de LaTeX. Par exemple comment fait on pour créer un nouveau paragraphe ?

C’est très simple, on saute une ligne. Cela termine le paragraphe courant et en commence un nouveau. En LaTeX un blanc est égal à plusieurs blancs ; les blancs en début de ligne sont totalement ignorés, de même que les blancs suivant un nom de macro 1 ; un saut de ligne est équivalent à un blanc à la règle ci-dessus près : deux (ou plus) sauts de lignes consécutifs ouvrent un nouveau paragraphe.

Enfin tous les caractères suivant un % et sur la même ligne, y compris le caractère de fin de ligne s o n t ignorés.

Caractères accentués

Une question intéressante : comment taper des caractères accentués si on n’a pas un clavier français ? On peut configurer un clavier américain pour obtenir les caractères accentués mais ça n’est pas toujours simple.

Une autre solution en LaTeX est d’obtenir les accents au moyen de commandes : la commande \' produit un accent aigu sur la lettre qui suit, si on tape par exemple \'elite, on obtient << élite >>. De même les commandes \` et \^ produisent respectivement un accent grave et un accent circonflexe (comme dans pêche et mèche) ; pour obtenir un c cédille on tape \c{c} (façon). Remarquons que ces commandes fonctionnent quelque soit la lettre que l’on accentue, par exemple on peut facilement faire À ou ñ, voire Ṕ (P accent aigu) ou O̧ (O cédille).

Jeu : deviner quelle commande produit le tréma.

Définitions

Ensemble bien ordonné

Définition 1. Un ensemble muni d’une relation d’ordre est bien ordonné si :

• la relation est totale ;

• toute partie non vide de a un plus petit élément.

Ordinaux

Définition 2. Un ordinal est un ensemble bien ordonné par la relation .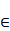

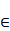Arithmétique ordinale

Théorème 1. Les opérations ordinales vérifient les propriétés suivantes :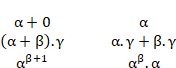

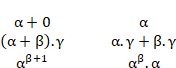
Exemple de suite de Goostein

$$\begin{array}{|c|c|c|} % trois colonnes centrées débutant, séparées et % finissant par des lignes verticales \hline % une ligne horizontale pour commencer le tableau j & G_i & i\\ % une ligne ; les colonnes sont séparées par &, la ligne est %terminée par \\ \hline \multicolumn{3}{c}{\strut}\\ % une ligne d'une seule colonne (centrée) % à la place de trois. La commande \strut % insère une espace vertical correspondant à % une ligne \hline 2 & 100 & 2\\ \hline 3 & 100 & 3\\ \hline \end{array} \qquad % insère une espace de deux quadratins entre les deux tableaux \begin{array}{|c|c|c|} \hline j & G_i & i\\ \hline \multicolumn{3}{c}{\strut}\\ \hline 2 & 100 & 2\\ \hline 3 & 100 & 3\\ \hline \end{array}$$

Quelques théorèmes qui n’ont rien à voir

Théorème 2. La formule d’Euler :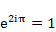

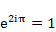
Proposition 3. La somme des premiers entiers est :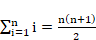

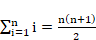
Cette propriété est fausse dans le cas des ordinaux (voir définition 2, page ).

Théorème 4 (Nombre d’or). Le développement en fraction continue du nombre d’or est : $$% L'environnement equation numérote % l'équation. L'étoile spécifie de ne pas mettre % de numéro \varphi = \cfrac 1{1+\cfrac 1{1 + \cfrac 1{1 + \dotsb}}}$$

Théorème 5. La fonction 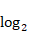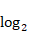définie par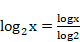 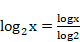est l’inverse (à droite) de la fonction « 2 puissance » :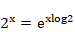

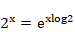
En effet on a le calcul suivant :

Et voici un dernier petit calcul pour la route, afin de montrer l’usage de l’environnement align. Ce calcul démontre que dans un anneau commutatif, 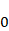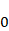(l’élément neutre de l’addition) est absorbant pour la multiplication :